Multigrid solver makes global forecasts quicker
August 2020 - recent Met Office research into multigrid solver techniques will result in faster global forecasts
Introduction
At the heart of the Unified Model (UM) lies its dynamical core, that part of the model responsible for solving the equations of large-scale fluid flow in the atmosphere on the model’s discrete mesh. One component of this dynamical core, which just by itself is computationally very expensive, is the subroutine which solves a very large number of coupled linear equations to obtain the pressure correction at each grid point during a model timestep. Recently a collaboration between the Met Office and the Department of Mathematical Sciences at the University of Bath led to the development and implementation of a more efficient solution method for the pressure correction equation in the UM. This new approach reduces the total runtime of the model significantly.
Current situation
In the current 10km resolution operational model, about 344 million coupled linear equations need to be solved to obtain the pressure correction in every timestep. This is currently done with an iterative method (the so-called BiCGStab iteration [van der Vorst, 1992]), which computes increasingly better approximations of the solution. A drawback of this approach is that every iteration requires global communications across all processors. Furthermore, for smaller tolerances on the error of the solution, the number of iterations increases substantially. Depending on the current state of the atmosphere, the number of solver iterations can also fluctuate, which has implications for predictability of the model runtime.
New multigrid solver
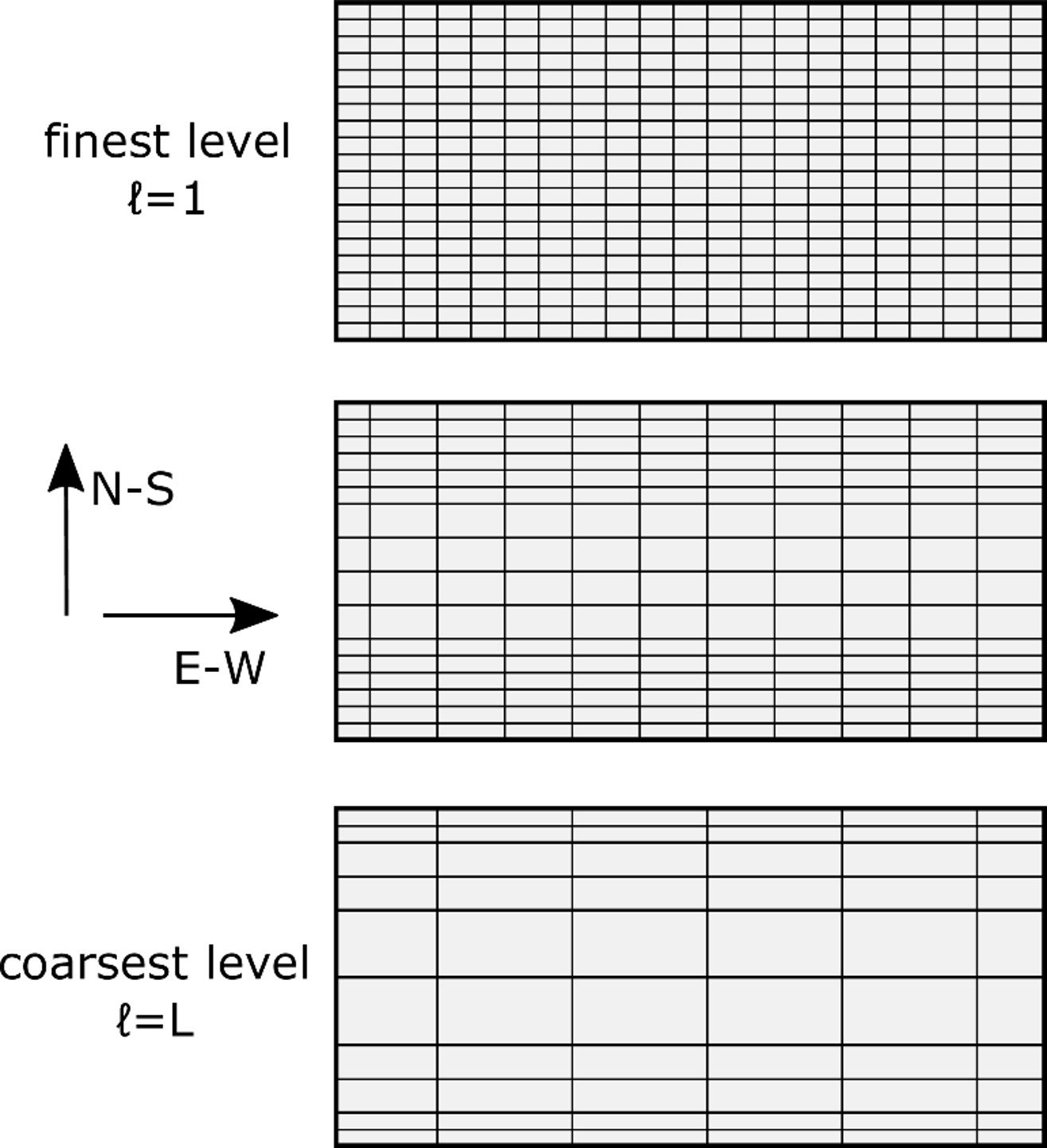
The multigrid technique (see Trottenberg et al. [2000] for an overview and Müller & Scheichl [2014] for a recent review of applications in atmospheric modelling) avoids those issues by solving approximations to the pressure correction equation on a hierarchy of coarser grids to correct the solution on the finest mesh. Since the coarse meshes contain less grid points and require less computation, this approach reduces the overall cost of the solver. Researchers at Bath developed a method for constructing optimal multigrid mesh hierarchies for the global latitude-longitude grid used in Numerical Weather Prediction [Buckeridge & Scheichl, 2010]. The key idea is to use conditional coarsening in the N-S direction while increasing the mesh spacing uniformly in the E-W direction. The Figure below shows an example of a semi-coarsened mesh. Using this approach, numerical issues due to the convergence of the grid lines at the poles (which results in the E-W grid spacing reducing significantly near the poles) can be addressed on the coarser grids.

Since multigrid reduces the error on all length scales simultaneously, it requires substantially less iterations and is more efficient overall: as demonstrated below, one linear solve with the new multigrid solver takes approximately half the time that was required with the previous BiCGStab method.
While currently multigrid has only been introduced for Global Models, work is under way to also implement this approach for Limited Area Models where horizontal boundary conditions have to be taken into account in the solver.
Performance
To quantify the magnitude of performance gains due to the new multigrid technology, tests have been run at all model resolutions relevant for the Met Office. In most cases multigrid leads to a sizeable reduction of the total model runtime compared to the current BiCGStab solver. For the current operational resolution (10km) on 1152 processors the time spent in a short 12-hour forecast is reduced from 39 minutes with the BiCGStab to 31 minutes with Multigrid. On 4608 processors a reduction of the runtime from 550 seconds (BiCGStab) to roughly 500 seconds (multigrid) is observed. For a very high-resolution model (6km) on 4608 cores the so-called “short forecast” run time decreases from 42 minutes to 32 minutes and on 18432 processors the run time changes from 11 minutes to 9.5 minutes.
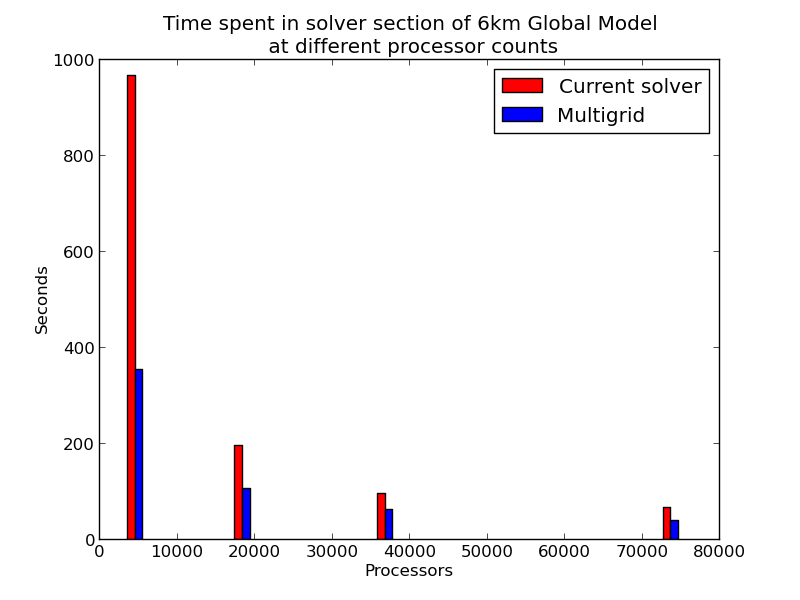
To compare the performance of the solvers directly it is also instructive to only measure the time spent in the solver subroutine. The Figure below shows this time for the current BiCGStab method and for multigrid on different processor counts for a 6km Global model run. The results in this plot confirm that the multigrid solver approximately halves the time spent on solving the pressure correction equation.

Because of those significant performance improvements, in the next upgrade to the operational forecast suite our main global model will use 8% less computational resource while the runtime is reduced by 2 minutes (45 minutes rather than 47 minutes). Lower resolution ensemble models will use about 10% less resource and be 7minutes faster (82 minutes compared to 89 minutes).
Verification and forecast quality
By producing a set of forecasts under realistic conditions and comparing to runs with the current model it was confirmed that the multigrid solver does not have a negative impact on forecast quality. This is to be expected since any differences in the results can be explained by the fact that the pressure correction equation is solved to the same finite tolerance with BiCGStab and multigrid, who will give slightly different but consistent approximations for the solution. As already expected from the experiments reported in the previous section, a significant reduction in runtime was also observed for forecasts under realistic conditions.
Conclusion
The collaborative efforts of the Met Office and the Department of Mathematical Sciences at the University of Bath have resulted in the implementation of a dramatically faster pressure correction solver in the Met Office Unified Model, which has a discernible impact on the total model runtime. The new multigrid solver will allow higher resolution forecasts to be run in the future and is already allowing better utilization of supercomputer resources.
Following the success of multigrid for the current ENDGame dynamical core, the Met Office are using the same solver technology for the next-generation LFRic model, which is based on an advanced finite element discretization on a cubed-sphere mesh. First tests have confirmed the superior performance of the multigrid approach [Maynard et al., 2020] in this setting.
References
- Buckeridge, S. and Scheichl, R., 2010. Parallel geometric multigrid for global weather prediction. Numerical Linear Algebra with Applications, 17(2‐3), pp.325-342.
- Maynard, C., Melvin, T. and Müller, E.H., 2020. Multigrid preconditioners for the mixed finite element dynamical core of the LFRic atmospheric model. To appear in Quarterly Journal of the Royal Meteorological Society, https://rmets.onlinelibrary.wiley.com/doi/10.1002/qj.3880
- Müller, E.H. and Scheichl, R., 2014. Massively parallel solvers for elliptic partial differential equations in numerical weather and climate prediction. Quarterly Journal of the Royal Meteorological Society, 140(685), pp.2608-2624.
- Trottenberg, U., Oosterlee, C.W. and Schuller, A., 2000. Multigrid. Elsevier.
- van der Vorst, H. A. 1992. Bi-CGSTAB: fast and smoothly converging variant of BiCG for the solution of nonsymmetric linear systems. SIAM J. Sci. Stat. Comput. 13, pp. 631-644.