Next generation atmospheric model development
May 2019 – Latest details on the development of the Met Office’s next generation atmospheric model, which uses GungHo and LFRic.
Introduction
At the heart of the Unified Model (UM) lies its dynamical core, that part of the model responsible for solving the equations governing fluid motion on the model’s discrete mesh. Recently two papers have been published, one that details the design of a proposed new dynamical core GungHo [1] and one that details a proposed new infrastructure LFRic [2] for the UM that can accommodate GungHo. This article briefly outlines the content of those papers, giving the background to, and design of, both GungHo and LFRic.
GungHo
In 2010, as the trend towards ever more massively parallel computers began to bite, it was recognised that in order to remain competitive into the future the UM had to become much more scalable. As a result, a 5-year project was initiated that was joint between the Met Office and UK academics (funded by NERC, the UK Natural Environment Research Council). The project became known as GungHo, after which the new dynamical core was named.
From the beginning, it was recognised that the principal driver for a further redesign of the dynamical core was the future of computer architectures. Therefore, co-design of the model with UK computational science experts (funded by STFC, the UK’s Science and Technology Facilities Council) was an essential element of the project and remains so today.
It was clear even before the start of the project that the principal bottleneck to achieving good scalability was the polar singularities of the latitude-longitude mesh employed in the UM (Fig 1, right). In the current 10 km global model, the latitudinal spacing between the row of grid points nearest each pole is a mere 13 m. This spacing reduces quadratically with increased resolution and so would be only 13 cm for a 1 km global model.
Therefore, a principal aim of the GungHo project was to decide on an alternative mesh to the current latitude-longitude one while retaining the beneficial accuracy and stability of the current model. One aspect of this was to avoid introducing computational modes (that would require numerical diffusion to control). A quadrilateral mesh became the preferred option.
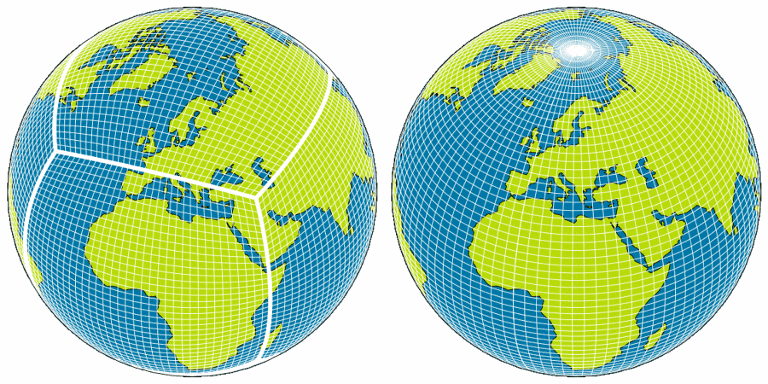
Fig 1: Example non-conformal cubed-sphere mesh (left) and traditional lat-lon mesh (right). The polar singularity in the lat-lon mesh is noticeable even in this low resolution example.
At the beginning of the project, a survey of the model users was undertaken to ask what their main requirements of the dynamical core were. By far the dominant requirement was improved, more local, mass conservation. This consideration together with the choice of a quadrilateral mesh led to the adoption of the cubed-sphere mesh rather than the alternative quadrilateral mesh known as Yin-Yang. A non-conformal cubed-sphere (Fig 1, left) was chosen in order to avoid the reintroduction of pole-like singularities at the corners (e.g. [3]).
A consequence of being non-conformal is that the coordinate lines are not orthogonal to each other. In contrast to the latitude-longitude mesh, this presents a number of challenges to achieving many of the essential and desirable properties of a dynamical core that GungHo targeted. Therefore, the choice was made to adopt the mixed finite-element method.
An important element of any dynamical core is its transport scheme. From the user survey, local conservation is an important consideration and suggested some form of flux scheme. Additionally, a significant contributor to the improvement in performance of dynamical cores over the last few decades has been the adoption of upstream-biased schemes. These have good dispersion properties together with the benefit of limited, but scale-selective, damping. It was therefore considered essential for GungHo to have the flexibility to use some form of finite-volume flux-form transport scheme independently of the choice of the particular mixed finite-element method chosen. This requires a conservative mapping between the finite elements and the appropriate finite volumes. Using (the target) lowest-order finite elements this mapping is trivial, and the approach has been shown to be effective for an Eulerian scheme (the implementation of a semi-Lagrangian flux form is underway). It remains to be seen whether the proposed technique can be extended successfully to allow coupling to higher-order mixed finite elements.
In summary, the proposed GungHo design is a semi-implicit temporal discretisation of a mixed finite-element spatial discretisation coupled with a flux-form finite-volume transport scheme. Early results are promising, and testing is now being extended to include the UM’s physical parametrisations.
LFRic
An important aspect of future-proofing the design of GungHo was the deliberate choice to keep as many options open as possible. Specifically:
-
A decision was made to use indirect addressing in the horizontal (exploiting the columnar nature of the mesh to amortise the cost of the indirect addressing). This approach makes it a lot easier (in principle at least!) to radically change the choice of the mesh without having to redesign and rewrite the whole model.
-
Although the target is a low-order finite-element scheme, the option to use higher orders has been retained. This is because it might be a way of reducing any undue grid imprinting due to the corners and edges of the sphere and it would also be necessary (to retain the desired numerical properties) if a triangular mesh were ever implemented.
-
The ability to support general families of finite-volume & finite-element discretisations has also been retained so that alternative dynamical core designs can be explored without having to rewrite the infrastructure.
The original motivation for GungHo was to improve the scalability of the UM’s dynamical core. However, as time has progressed it has become evident that not only are supercomputers providing more and more cores (and hence the scaling problem) but the nature of those cores is also changing (to make them more energy efficient). Supercomputer architectures are becoming more and more heterogeneous (for example as GPUs become incorporated into CPUs). Also, those processors are supported by deeper and deeper hierarchies of memory. Further, it remains unclear exactly what the architectures of the mid-2020s and beyond will look like. It is becoming essential therefore that, whatever the scientific design of the dynamical core, its technical implementation must be, as far as possible, agnostic about the supercomputer architecture that it is designed for.
This realisation came at a time when it became clear that to implement GungHo within the UM would require two major changes. The first would be a move away from direct indexing permitted by the use of a latitude-longitude mesh (in which each direction is independently referenced) to indirect addressing. The second would be the move away from the finite-difference scheme to a finite-element scheme. The UM was fundamentally built and designed around direct addressing and finite-difference numerics. Additionally, it was originally designed some 25 years ago (see [4] for a historical perspective). The bold decision was therefore made to design, develop and implement a new model infrastructure with the specific aim of being as agnostic as possible about the supercomputer architectures. This project is a joint project between the Met Office and STFC, and it is called LFRic after Lewis Fry Richardson who made the first steps towards numerical weather prediction decades before the first computers were available.
At the heart of LFRic is an implementation (named PSyKAl) of the principle of a ‘separation of concerns’ between the algorithms and the code needed to implement those algorithms efficiently on future supercomputers. In this approach, a model time step is separated into three layers: Parallel Systems; Kernels; and Algorithms (Fig 2). In the Algorithm layer, only global fields are manipulated without any reference to specific elements of those fields. The Kernel layer operates on whatever the smallest chunk of model memory is. For LFRic this is currently a single column of data. It is the job of the PSy layer to dereference the specific elements of the global fields and ensure that they are distributed appropriately to the relevant pieces of computational hardware. Therefore, it is the PSy layer that implements all the calls to MPI, including the necessary halo exchanges etc., and that also implements the directives for OpenMP, including colouring where necessary (to avoid contentions). Work is underway to make use of OpenACC in order to target GPUs.
This approach means that the science code can be implemented independently from whatever aspects are required to make the model run on a parallel machine. This makes the parallel aspects less prone to programming errors by scientists, and it also avoids the habit of putting in redundant halo exchanges ‘just in case’ with the associated inefficiencies.
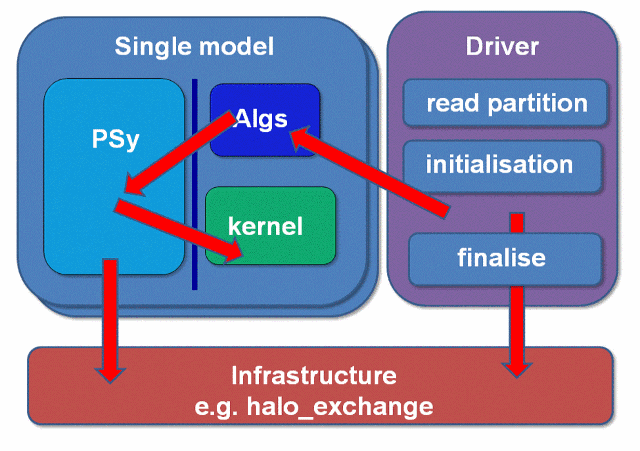
Fig 2: Schematic diagram of the PSyKAl layered architecture. A single model could be for example, the atmospheric model. The blue vertical line between the PSy layer and the Algorithm and Kernel layers represents a separation of the science and parallel code. Red arrows indicate the flow of data through the model.
The key aspect of this approach is that the PSy layer is autogenerated by the open-source Python package PSyclone, owned and developed by STFC. This relies on there being a strict interface (an API) between each of the layers together with appropriate, supporting metadata. The autogeneration of code means that only one source code needs to be maintained; the modifications to that code, which are needed for it to run optimally on any specific supercomputer architecture, are created by the autogeneration tool without changing the original source code.
Additionally, any generic or machine-specific optimisations can be constructed from PSyclone transformations, again without polluting the Algorithms and the Kernels where the science code lives. As well as being flexible in terms of future supercomputer architectures, the approach also means that the model can be run efficiently across a range of contemporaneous architectures without requiring invasive changes to the source code.
As an illustration of the effectiveness and utility of this approach, it took less than two weeks for the original, serial version of GungHo to be able to run in parallel on 220,000 cores of the Met Office Cray XC40 once PSyclone support for distributed memory was available.
Summary
Developing a dynamical core that is suitable for operational, unified modelling across spatial scales ranging from below urban scales O(100m) to planetary scales O(1000km), and across temporal scales ranging from a few minutes to centuries, is challenging. It puts strong constraints on both the continuous equation set used and the combination of numerical methods used to discretise those equations. In this regard, the semi-implicit semi-Lagrangian scheme, applied to the almost unapproximated deep-atmosphere, nonhydrostatic equations, has served the Met Office well for over 15 years.
An additional emerging challenge is to make the model scalable when run on the massively parallel supercomputers of today, as well as ensuring that the models will continue to be efficient on whatever the next generation of supercomputer architectures will look like.
The combination of the GungHo dynamical core with the LFRic modelling framework attempts to rise to those challenges. The result is a mixed finite-element, finite-volume, semi-implicit scheme implemented within a modern, flexible, object-oriented, software infrastructure designed using the concept of a separation of concerns.
References
[1] Melvin T, Benacchio T, Shipway B, Wood N, Thuburn J, Cotter C (2019): A mixed finite-element, finite-volume, semi-implicit discretisation for atmospheric dynamics: Cartesian geometry. Quarterly Journal of the Royal Meteorological Society. 145. https://doi.org/10.1002/qj.3501
[2] Adams SV, Ford RW, Hambley M, Hobson JM, Kavčič I, Maynard CM, Melvin T, Müller EH, Mullerworth S, Porter AR, Rezny M, Shipway BJ and Wong R (2019): LFRic: Meeting the challenges of scalability and performance portability in Weather and Climate models. Journal of Parallel and Distributed Computing. https://doi.org/10.1016/j.jpdc.2019.02.007
[3] Staniforth A and Thuburn J (2012): Horizontal grids for global weather and climate prediction models: a review. Quarterly Journal of the Royal Meteorological Society. 138. 1-26. https://doi.org/10.1002/qj.958
[4] Brown A, Milton S, Cullen M, Golding B, Mitchell J, Shelly A (2012): Unified Modeling and Prediction of Weather and Climate: A 25-Year Journey. Bulletin of the American Meteorological Society. 93. 1865–1877. http://dx.doi.org/10.1175/BAMS-D-12-00018.1