Sea ice: an overview
Sea ice is a critical component of the Earth's climate system and has a wide-reaching impact beyond the polar regions.
Sea ice is frozen seawater which floats on the surface of the ocean. Sea ice occurs in both the Arctic and Antarctic where little or no sunlight means that atmospheric conditions are cold enough for the ocean to freeze in the winter.
Sea ice composition
Sea ice consists of blocks of frozen seawater known as "floes", which are always in motion pushed along by winds and ocean currents. Sea ice floes range in size between 10 m and 5 km wide and are of the order of 0.5 to 5 m thick. Areas of open water between ice floes are called "leads". Snowfall remains on the floes all year round and over winter can get to 10-20 cm deep. Sea ice floes can freeze together and can be broken by collisions or ocean waves. Depending on the time of year and the location, ice floes may float independently from each other or be squashed together to form an almost continuous pack ice cover permeated by cracks and ridges of thicker ice.

The chaotic looking ature of sea ice is an artefact of the complicated way in which seawater freezes and the presence of waves and currents on the surface of the ocean. To illustrate the difference between freshwater and seawater we first consider more generally the processes that happen when water is cooled to freezing point from above. In general as freshwater cools its density increases. This means that water that is cooled from above by the atmosphere sinks and is replaced by more buoyant, warmer water from below. As the water continues to be cooled from above this combined cooling and mixing (or convection) process persists until the water reaches its temperature of maximum density - below which the water actually becomes less dense with further cooling. By a quirk of physics freshwater reaches its maximum density at about 4° Celsius. Beyond this point the cooling water no longer sinks and so it is possible to freeze the surface layer(s) of a freshwater lake or pond almost uniformly as a nice flat stable layer of ice (which floats because it is less dense than the water below).
Freezing temperature versus temperature of maximum density for saline water
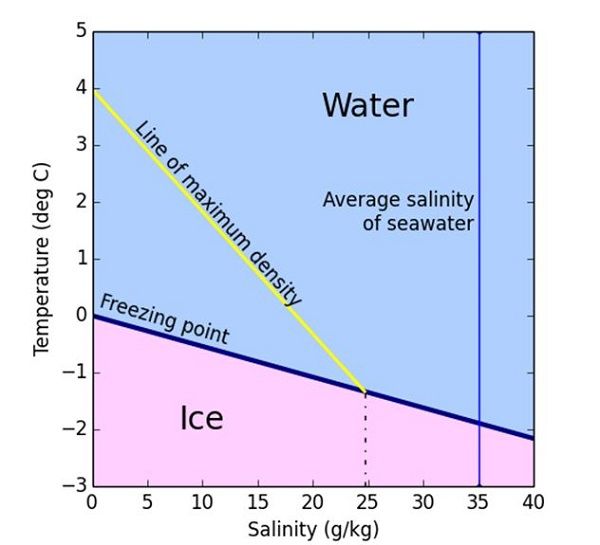
Figure 1: Freezing temperature (blue line) versus temperature of maximum density (yellow line) for saline water.
However the presence of salt in seawater changes all of this. Whilst the freezing point of freshwater is 0° C, the salt forces the freezing point of seawater to be lower (see the blue line in Figure 1). Typically seawater with a salinity, or salt content, of 35 parts per thousand (or 3.5%) will have a freezing point of around -1.8° C. The point of maximum density for seawater also decreases with increasing salinity but at a faster rate than the freezing temperature does; this is shown by the yellow line in Figure 1. For salt water with salinity above 24.7 parts per thousand the temperature of maximum density is below the freezing temperature. The majority of seawater has salinity above 24.7 which means that sea water cooled from above continues to cause convection right down to the freezing point. This means that sea ice does not form in a uniform way like freshwater ice and is much more complicated.

When the ocean starts to freeze, ice initially takes the form of lots of little crystal discs called 'frazil', which float independently on the sea surface. As more ice crystals grow they form a suspension in the surface water known as 'grease ice' (owing to the way its surface resembles an oil slick). In calm conditions these ice crystals can freeze together to form a continuous expanse of, initially transparent, thin ice (just a few millimetres thick) called 'nilas'. In more turbulent waters however, the waves and wind act to compress the tiny frazil crystals into larger circular structures known as 'pancake ice'. These 'pancakes', which can sometimes be several metres in diameter, float on the ocean surface, colliding with one another and, over time, can become frozen together to form sea ice floes with a very rough appearance.

Once nilas or pancake ice has formed, seawater can freeze on to the bottom of it causing the ice to thicken through a process known as 'congelation growth'. Congelation growth traps pockets of seawater and air bubbles within the ice as it freezes. These bubbles are responsible for the opaque nature of sea ice which generally has a white, matt appearance when compared with freshwater ice. As the atmosphere (which may be colder than -40° C) continues to cool the ice from above, much of the water contained within these pockets freezes causing the pockets to contract into tiny bubbles of very salty water called 'brine'. The presence of numerous brine bubbles within the ice means that sea ice is generally weaker and more 'mushy' than freshwater ice. As the ice grows brine is expelled from the sea ice floes through a series of processes known collectively as 'brine rejection'. This means that as sea ice ages its strength increases.

As well as thermodynamic ice growth such as congelation, thicker ice can also be formed when sea ice floes collide via dynamic processes known as 'ridging' or 'rafting'. Ridging can occur when relatively thick floes collide and ice is simultaneously forced upwards to create sails (~2 m high) and downwards to create keels (~10 m deep). Normally the force of the collision is greater than the tensile strength that the ice can sustain and so the ice often breaks up. This means that new ridges often look similar to piles of 'ice rubble' just sitting upon the sea ice. Rafting meanwhile occurs when two relatively thin ice floes collide and slide across each another such that they are stacked one on top of the other. In addition to the pack ice that drifts on top of the ocean, land-fast ice (or 'fast ice') occurs in shallow and/or coastal areas when sea ice is either held fast to the coastline of when ice keels run aground on the sea bed.
Sea ice: a year in the life
Sea ice cover varies seasonally with a maximum cover occurring during early spring and a minimum cover during early autumn. This seasonality is caused by the amount of sunlight reaching the polar regions of the Earth which are virtually dark for 4 months over winter and light throughout the day for much of the summer.
During the winter, in the absence of any sunlight, the sea ice insulates the ocean from the much colder atmospheric temperatures above. Snowfall through the winter months accumulates upon the sea ice which increases this insulating affect. However the sea ice is not able to completely insulate the ocean from the subzero temperatures above and so the ocean will freeze at the base of the sea ice causing the ice to thicken. Thicker ice is a better insulator than thinner ice and so thin ice tends to increase in thickness at a faster rate than thicker ice. As winter draws to an end and spring starts the sea ice cover reaches its maximum extent for the year. This will normally be in February in the Northern Hemisphere (Arctic) and September in the Southern Hemisphere (Antarctic). After this point the net growth of the ice will be less than the net melting of the ice and so the ice cover starts to decline.
ice albedo feedback
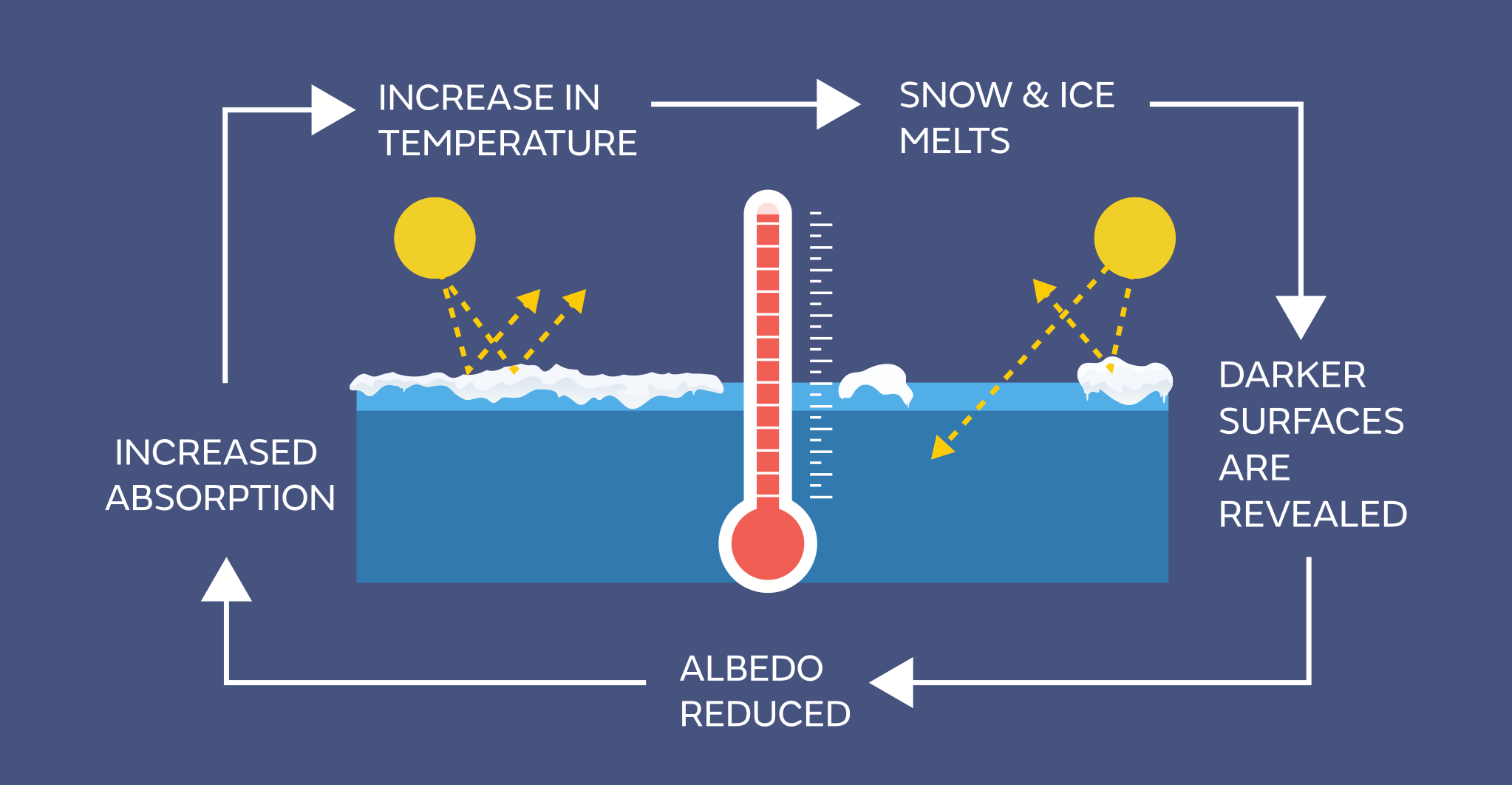
Figure 2: Schematic showing the ice albedo feedback which can lead to amplification of warming in the Arctic.
Once the sun rises sufficiently above the horizon to warm the surface in late spring, the ice starts to melt more intensely. Being less reflective than the sea ice floes, the leads absorb sunlight into the ocean which causes the sea ice to melt from below. The melting ice causes the leads to increase in size to create larger areas of open water. This allows more solar radiation to be absorbed which in turn causes increased melting. This mechanism is known as the "ice-albedo feedback" and is depicted in Figure 2. This ice-albedo mechanism is also important for melting processes on the top of the sea ice because the albedo (or reflectivity) of snow and ice is lower when it is melting. One key aspect of the melting cycle is the presence of surface melt ponds upon the sea ice. These ponds are caused by melting of the accumulated snow cover and are formed when melt water is bounded by snow on all sides and so remain on top of the sea ice. As these ponds are formed of liquid water they are less reflective than the surrounding snow and ice and so they absorb more solar radiation. This causes the melt ponds to grow horizontally and also thins the sea ice below them. Melt ponds upon the sea ice are common place during the summer months, particularly in the Arctic.
Melting of the sea ice continues through the summer until the reduced solar heating, caused by the changing of the seasons, once again means that the net rate of freezing outweighs that of melting and so the sea ice cover grows once again. This summer minimum of ice cover will normally occur in September for the Northern Hemisphere (Arctic) and in February for the Southern Hemisphere (Antarctic). After the summer minimum the sea ice continues to grow as more and more of the ocean is frozen. As winter approaches the amount of sunlight reaching the polar ocean reduces to nothing.
Average Arctic sea ice over the period 1981-2010
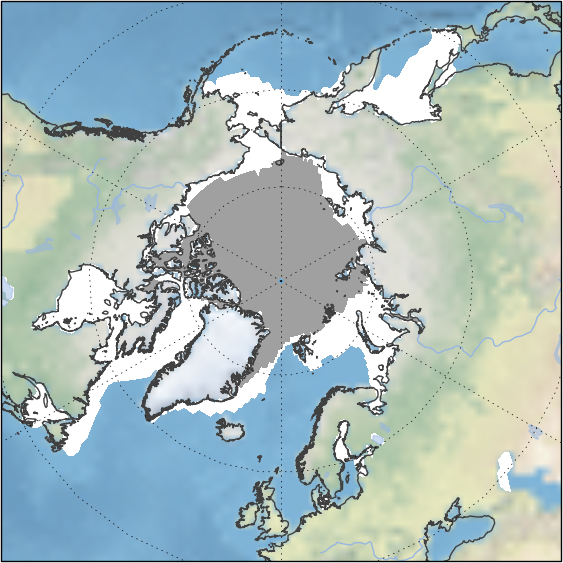
Figure 3: Average Arctic sea ice summer minimum (grey) and winter maximum (white) over the period 1981-2010. Data are from Met Office Hadley Centre HadISST dataset.
Arctic sea ice
Arctic sea ice reaches a maximum extent of about 15-16 million square km in February or March and a minimum extent of about 5-6 million square km in September. Figure 3 shows the average summer minimum and winter maximum Arctic sea ice cover for the period 1981-2010.
The September minimum extent is heavily dependent on weather conditions, as the ice is thin and easily broken, and is therefore more variable than the winter maximum (which is constrained by the area of winter darkness and warm ocean currents). Figure 4 shows the seasonal cycle for various periods derived from satellite measurements. Notably not all of the Arctic sea ice is melted each year and much of it persists through the summer to form 'multi-year' ice. Multi-year ice tends to be thicker than new first year ice and, owing to brine rejection, has a higher mechanical strength. As sea ice is more reflective than the surrounding ocean, the existence of multi-year ice through the summer months is an important regulator of climate conditions in the Arctic.
Seasonal cycle of Arctic sea ice cover
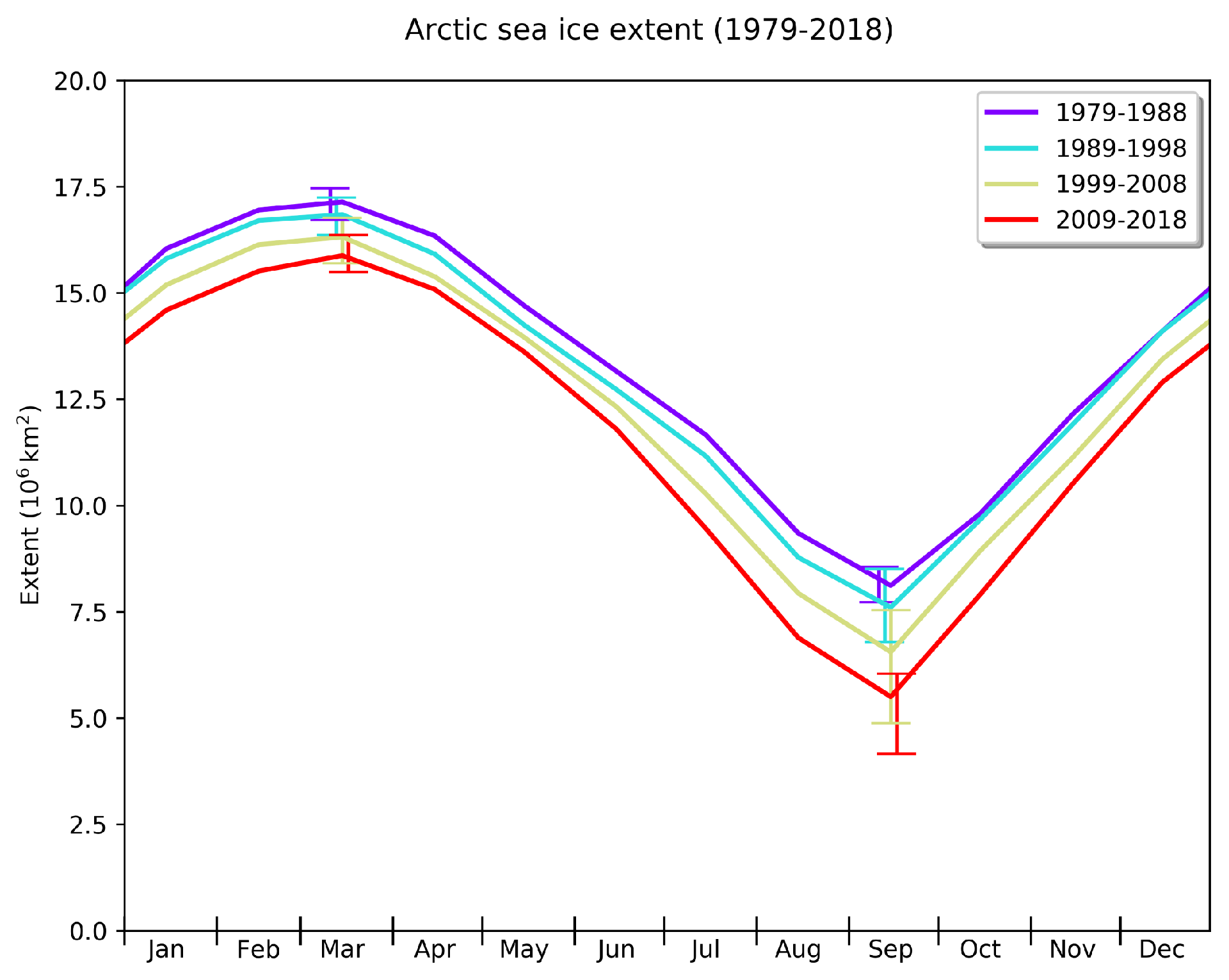
Figure 4: Seasonal cycle of Arctic sea ice cover illustrated by decadal averages of daily extent. Data are from Met Office Hadley Centre HadISST dataset.
Map of average sea ice movement in the Arctic
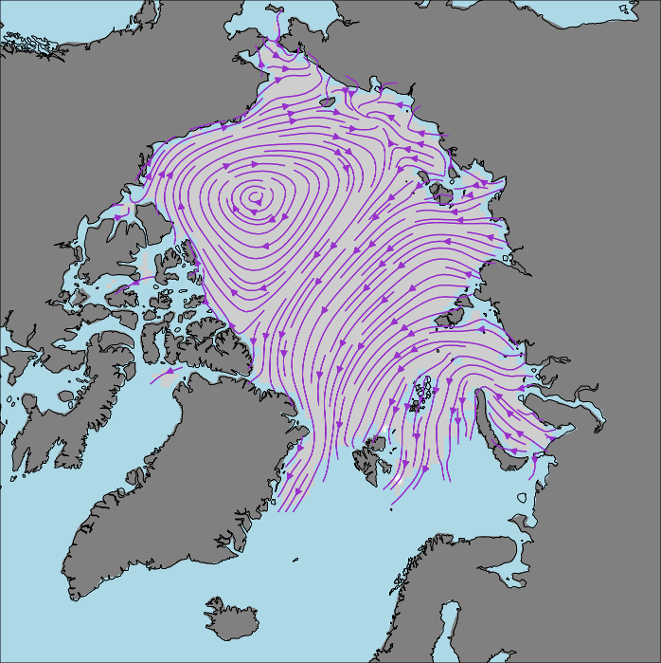
Figure 5: Map of average sea ice movement in the Arctic derived from satellite measurements. Data from the Copernicus Marine Environment Monitoring Service (CMEMS).
Arctic sea ice motion is restricted by the geometry of the Arctic Ocean and the prevailing wind and currents. The predominant circulation features in the Arctic sea ice (see Figure 5) consist of a transpolar drift across the European side of the Arctic together with a weaker anti-cyclonic (clockwise) recirculation in the Beaufort Sea in the North American Arctic (around the Beaufort Gyre). The transpolar drift transports ice from the Siberian coastline and Eurasian marginal seas across the Arctic Ocean towards the northeast coast of Greenland and the Fram Strait - which separates Greenland from the Svalbard Archipelago to the east (see Figure 6). Any ice passing through the Fram Strait results in export of sea ice from the Arctic Ocean and down the east coast of Greenland, eventually to melt in the warmer Atlantic waters. Ice that is not exported from the Arctic tends to pile up against the northern coasts of Greenland and the Canadian Arctic Archipelago. This means that sea ice is generally thicker in these areas as can be seen in Figure 7 which shows average sea ice thickness during winter 2013 measured from space.
Map of the Arctic region
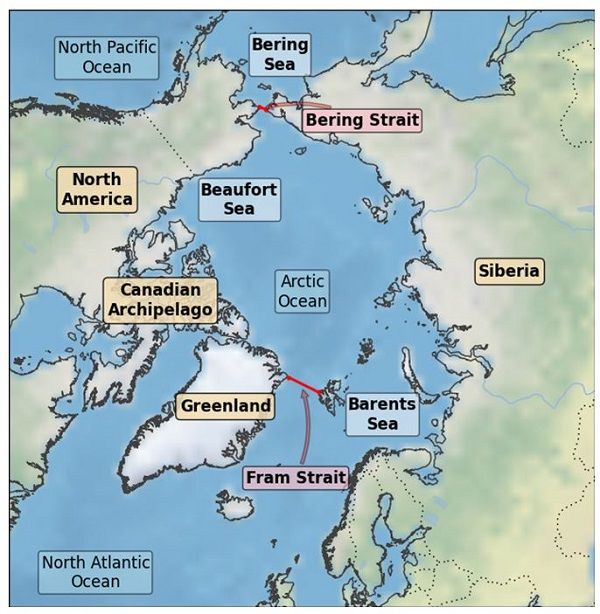
Figure 6: Map of the Arctic region with land masses, ocean basins, regional seas and straits labelled.
What factors can cause variations in Arctic sea ice?
Arctic sea ice is heavily influenced by the seasonality the atmosphere and the ocean. After the aforementioned seasonal changes in solar heating, interaction with the wind is the next most important driver of Arctic sea ice behaviour. In particular storms penetrating the ice pack can break it up, changing the heat transfer from the ocean to the atmosphere. They can also bring snow with them and when this falls upon the sea ice it increases the insulating properties of the ice thus reducing ocean heat loss. Storms can also draw up warmer water from the deeper ocean to the surface which can melt the sea ice. Heat loss from the ocean to the atmosphere in the wake of a storm cools the ocean forming new or thicker ice.
Clouds also have a strong impact on the sea ice. In the summer they reflect sunlight, reducing the amount available to melt the ice and in the winter the clouds act as a blanket that insulates the lower atmosphere and ocean, causing reduced ice growth. Most of the fresh water in the Arctic comes from rivers and so an increase in rainfall over Eurasia or North America can make the ocean surface layer fresher. A fresher surface means less mixing in the ocean and hence less warm water reaching the surface to melt the ice. A fresh ocean surface in the autumn means that sea ice can form more easily and faster as the ocean cools.
The sea ice cover is also affected by the transport of warmer waters from lower latitudes into the Arctic Ocean. In particular water from the Atlantic Ocean enters the Arctic through the Greenland, Icelandic and Norwegian Seas. Usually this water is more salty, and hence denser, than Arctic Ocean water and so flows underneath it. This warmer water then circulates around the Arctic, taking about 7 years to do so, before exiting back into the Atlantic in the form of cooler surface waters. As it circulates around the Arctic the warm Atlantic water releases its heat, which can melt the sea ice from below. The winds in the Greenland Sea drive the warm water into the Arctic and the strength of these winds, and hence the amount of ocean heat available to melt ice, depends on the North Atlantic Oscillation. Warmer waters can also enter the Arctic Ocean from the Pacific Ocean through the Bering Strait between Alaska and Siberia (see Figure 6). The amount of ocean heat passing through the Bering Strait depends on the position of the Aleutian Low - the dominant atmospheric pressure system in the North Pacific. The Bering Sea is relatively shallow (about 100m), and so warmer water blown into the Arctic from the Pacific will be close to the surface of the ocean where it can directly melt the sea ice.
Arctic sea ice average thickness for winter 2013
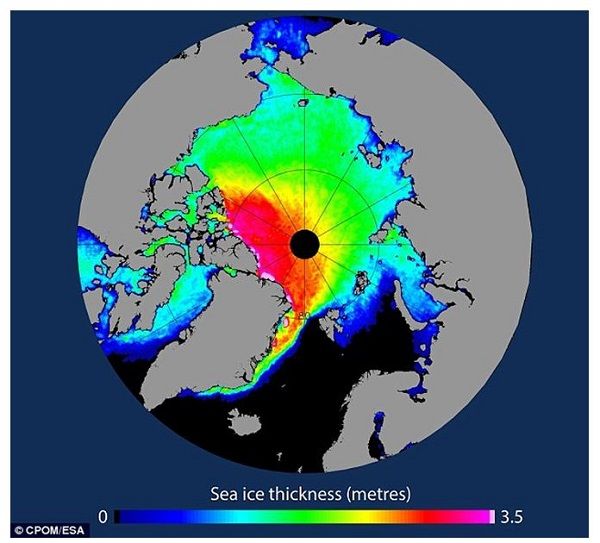
Figure 7: Arctic sea ice average thickness for winter 2013 measured by ESA's CryoSat-2 satellite. (Image courtesy CPOM &
The Arctic energy budget
The Arctic is not a closed system and the transfer of heat energy into, and out of, the region is important for the energy balance of the planet. Figure 8 shows a schematic representation of the main components of the energy budget of the Arctic. The arrows represent the direction of net energy transfer and the relative size of each arrow shows the amount of energy transferred. The dominant terms are the net loss of heat from the atmosphere to space from the Arctic and the net input of energy from lower latitudes via the atmosphere.
Heat transport into the region from lower latitudes by the atmosphere and, to a lesser extent, the ocean make up a large part of the energy balance of the Arctic. Heat is constantly being transferred to the Arctic from mid-latitudes by the exchange of warm air moving north and cold air moving south, often during the passage of storms. Heat also enters the Arctic through the ocean, as northward-moving currents bring warmer water into the Arctic Ocean. The wind-driven export of sea ice from the Arctic Ocean also represents a net gain in heat energy for the region (because the sea ice will have released energy when it formed and would require heat energy to melt).
Within the Arctic the net transfer of energy is from the ocean to the atmosphere - and via the sea ice where present. In the Arctic the ocean surface is generally warmer than the colder atmosphere above. When open water forms heat loss from the (relatively) warm water to the cold air above is mostly rapid and powerful, although the summer, when atmospheric cooling is at its lowest, the open sea can instead gain energy through the absorption of sunlight. However, over the course of a year, there is a net transfer of heat from the ocean to the atmosphere. Being warmer than the sea ice, the ocean transfers energy to the sea ice throughout the year, warming the ice and melting it from below. The sea ice in turn loses energy to the cold atmosphere through thermal radiation for most of the year, although this process is briefly reversed during the summer.
On average the Arctic loses far more heat energy to space in thermal radiation than it gains in sunlight. The reason for this is partly the fact that the Arctic is dark throughout the winter months but also because the high albedo of sea ice and snow causes much of the sun's rays to be reflected back into space. The Arctic therefore is an area of net heat loss from the atmosphere into space which makes it important for regulation of the Earth's climate.
Schematic showing Arctic energy balance
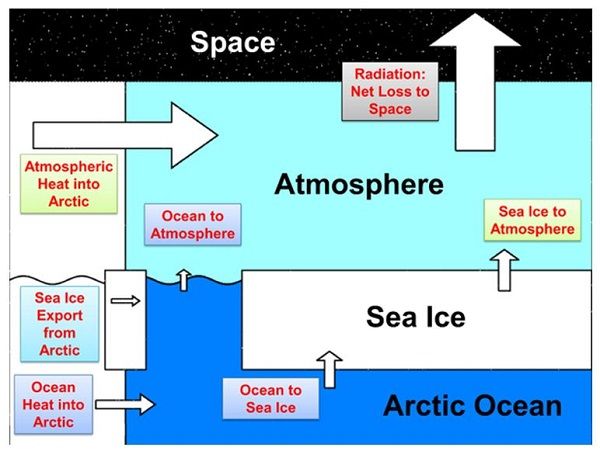
Figure 8: Arctic energy balance schematic showing the transfer of energy into, and out of, the Arctic as well as between the ocean, sea ice and atmosphere. Arrow size is representative of the magnitude of each term.
Predictability of Arctic sea ice
The ability to predict the sea ice state months in advance is useful for determining shipping routes and the productivity of fisheries. However the strong influence of the winds and clouds on the growth, melt and movement of Arctic sea ice, mean that regional weather conditions play a key role in determining the sea ice state. Owing to the difficulties associated with predicting the weather more than a few days ahead, prediction of Arctic sea ice on monthly and seasonal time scales is a very challenging undertaking.
However there are some large-scale atmospheric states which influence the Arctic sea ice that may be predictable, such as the winter North Atlantic Oscillation and the position of the storm tracks. In addition, there are some characteristics of the sea ice that essentially accumulate the impact of the weather. For example the thickness of sea ice changes slowly and so initialising a model forecast using observations of ice thickness could increase predictability of sea ice extent on seasonal time scales and beyond. Another potentially useful seasonal sea ice predictor is the melt pond coverage in June. A large number of melt ponds in the snow cover upon sea ice means that a lot of heat has gone into the ice, either because spring came early or summer has been particularly warm.
There is Arctic sea ice about Met Office involvement in forecasting the summer minimum extent of Arctic sea ice on seasonal time scales as part of the global Sea Ice Prediction Network (SIPN) .
References
Wadhams, Peter. "Ice in the Ocean." CRC Press, 2000.





